The “Injectivity Implies Surjectivity” Trick

There is a standard proof technique involving the relationship between injectivity and surjectivity on “finite” structures. I rather like it—for the examples provided, it is very difficult to proceed without knowing the trick, even though the solutions are very simple.

Principle A: If $S$ is a finite set and $\phi: S\to S$ is a function, then $\phi$ is injective if and only if $\phi$ is surjective.

Proposition 1: If $\mathbb{F}$ is a finite field and $\phi:\mathbb{F}\to\mathbb{F}$ is a homomorphism of fields, then $\phi$ is an isomorphism.

Proof: $\ker{\phi}$ is an ideal of $\mathbb{F}$ , but it cannot equal $\mathbb{F}$ , (for $\phi(1)=1$ ) so $\ker{\phi}=0$ and $\phi$ is injective. Therefore $\phi$ is surjective.

Proposition 2: If $G$ is a finite simple group and $\phi:G\to G$ is a homomorphism, then $\phi$ is an isomorphism or $\phi\equiv e$ .

Proof: Either $\ker{\phi}=G$ , in which case $\phi\equiv e$ , or $\ker{\phi}=\{e\}$ , in which case $\phi$ is injective, so $\phi$ is surjective.

Principle B: If $V$ is a finite dimensional vector space and $\phi:V\to V$ is a linear transformation, then $\phi$ is injective if and only if $\phi$ is surjective.

Proposition 3: If $K$ is a field and $A$ is an integral domain containing $K$ with finite dimension over $K$ , then $A$ is a field.

Proof: It suffices to show that we can take inverses. Choose any nonzero $a\in A$ , and consider the map $\phi: A\to A$ defined by $\phi(x) = ax$ . Then $\phi$ is a linear transformation. Since $A$ is an integral domain, $\phi$ is injective, therefore $\phi$ is surjective. So there exists some $b\in A$ with $\phi(b)=1$ , so $ab=1$ .

Problem: Show that any finite integral domain is a field.

EDIT: As Steven points out in the comments, the following is also useful, and the proof is a good exercise:

Principle C: If $M$ is a Notherian module then any surjective homomorphism $\phi: M\to M$ is injective, and if $M$ is an Artinian module, then any injective homomorphism $\phi:M\to M$ is surjective. (hint: in fact, for any $\phi:M\to M$ , if $M$ is Noetherian, then for large enough $n$ we have $\ker{\phi^n} \cap \rm{image}\ \phi^n = 0$ . If $M$ is Artinian, then for large enough $n$ we have $\ker{\phi^n} + \rm{image}\ \phi^n = M$ .)

This entry was posted on Saturday, October 18th, 2008 at 8:32 pm and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

6 Responses to The “Injectivity Implies Surjectivity” Trick

Steven Sam says:

October 19, 2008 at 2:36 am

It may be worth mentioning other instances of this:

Let $M$ be an $A$-module, and $u \colon M \to M$ an endomorphism. Then$u$ surjective and $M$ Noetherian implies $u$ is injective. Similarly, $u$ injective and $M$ Artinian implies $u$ is surjective. ($A$ can be any commutative ring). This is Exercise 6.1 of Atiyah–MacDonald.

Reply
lydianrain says:

October 19, 2008 at 3:23 am

Yes, that’s a good idea–I’ll add an edit. I’ve seen the first one before in Dummit and Foote–the second one is new to me. (though I see that the proof is the same)

Reply
David Speyer says:

January 30, 2009 at 7:15 pm

It’s also worth mentioning the amazing result of Ax:

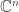If $F$ is an injective polynomial map from $\mathbb{C}^n$ to itself, then $F$ is surjective. The proof (1) uses model theory to replace the complex numbers by the algebraic closure of a finite field, (2) uses an elementary argument to replace the algebraic closure of a finite field by a finite extension of the finite field (3) uses the obvious observation above.

Reply
- lydianrain says:
  
  January 30, 2009 at 7:24 pm
  
  Thanks–I learned this result in model theory but forgot all about it for this post!
  
  Reply
theo says:

October 3, 2012 at 8:09 am

Are there ‘tricks’ like these for morphisms of finitely generated algebras? I’m guessing fg is not finite enough, but just wanted to check if any positive results are known.

Reply
- lydianrain says:
  
  October 4, 2012 at 1:52 am
  
  I guess there are a number of theorems in algebraic geometry with this general flavor, but I don’t know of any direct analogies.
  
  The closest analogy I can think of is for modules over nice rings. For example, Atiyah-MacDonald has a number of similar results and exercises about modules over local rings.
  
  Reply